Rappels de trigonométrie
Un aide mémoire pour les fonctions et les identités trigonométriques se trouve dans l’annexe E, à la page 562 du livre de Lafrance.
Rapports trigonométriques
Les fonctions trigonométriques permettent de calculer les rapports des côtés d’un triangle rectangle. Un truc mnémotechnique pour vous rappeler des définitions est SOH CAH TOA :
\[\begin{align*} \sin\theta &= \frac{\mathrm{Opp}}{\mathrm{Hyp}}, & \cos\theta &= \frac{\mathrm{Adj}}{\mathrm{Hyp}}, & \tan\theta &= \frac{\sin\theta}{\cos\theta} = \frac{\mathrm{Opp}}{\mathrm{Adj}}. \end{align*}\]
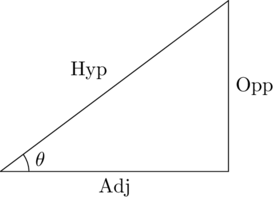
Figure .: Triangle rectangle utilisé pour définir les rapport trigonométriques.
Cercle unitaire et identités trigonométriques
Le cercle unitaire est un cercle de rayon \(1\) centré à l’origine d’un système de coordonnées cartésien. L’angle correspondant à un point sur le cercle est entre l’axe des \(x\) positifs et un segment de droite reliant l’origine au point. Les coordonnées de ce point sont le cosinus et le sinus de l’angle correspondant. Par convention, un angle mesuré en tournant dans le sens anti-horaire est positif alors qu’un angle mesuré en tournant dans le sens horaire est négatif.
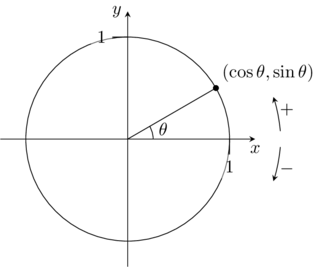
Figure .: Cercle unitaire.
Si on compare les deux triangles identifiés dans la figure ci-dessous, on constate qu’ils sont identiques et que le côté long du triangle vert correspond à \(\cos\theta\) alors que le côté long du triangle bleu correspond à \(\sin(\theta + \pi/2)\). Par conséquent
\[\sin(\theta + \pi/2) = \cos\theta.\]
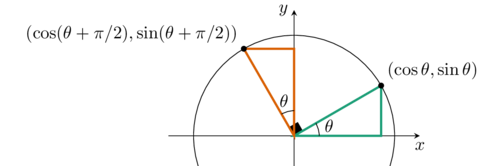
Figure .: Lien entre le sinus et le cosinus de deux angles qui diffèrent de 90 degrés.
En appliquant le théorème de Pythagore à un triangle rectangle inscrit dans le cercle trigonométrique, on obtient directement l’identité suivante :
\[\cos^2\theta + \sin^2\theta = 1\]
Fonction trigonométriques
Vous pouvez consulter le site alloprof pour avoir accès à plusieurs pages de révision sur les fonctions trigonométriques. Ici, je me contente de vous rappeler brièvement les points les plus importants.
En mathématique, vous avez probablement vu la forme canonique de la fonction cosinus : \[f(x) = a \cos(b(x - h)) + k.\] Le paramètre \(a\) correspond à l’amplitude, le paramètre \(b\) est relié à la fréquence, le paramètre \(h\) est le décalage horizontal de la fonction et le paramètre \(k\) est le décalage vertical de la fonction. Dans le cours de physique, nous utiliserons des noms légèrement différents pour ces paramètres et ils seront associés à des significations physiques précises. Nous en reparlerons en détail dans les deux premiers chapitres du cours.
\(f(x) =\) \(\cos(\) \((x -\) \()) +\)
\(g(x) = \cos(x)\)
\(a\)
\(b\)
\(h\)
\(k\)
Fonctions trigonométriques inverses
Les fonctions trigonométriques inverses permettent d’obtenir un angle à partir de la valeur d’un rapport trigonométrique.
\[\begin{align*} \arccos x = \theta \;\mathrm{ssi}\; & x = \cos\theta \\ & \mathrm{et}\; \theta \in [0, \pi] \end{align*}\]
\[\begin{align*} \arcsin y = \theta \;\mathrm{ssi}\; & y = \sin\theta \\ & \mathrm{et}\; \theta \in [-\pi/2, \pi/2] \end{align*}\]
\[\begin{align*} \arctan z = \theta \;\mathrm{ssi}\; & z = \tan\theta \\ & \mathrm{et}\; \theta \in [-\pi/2, \pi/2] \end{align*}\]
Les fonctions trigonométriques inverses ne donnent qu’un seul angle. Il faut utiliser le cercle trigonométrique pour déterminer les autres angles admissibles.
Deux angles avec le même cosinus
Les deux angles entre 0 et \(2\pi\) qui donnent le même cosinus ont la même coordonnée en \(x\). Par conséquent, si \(\arccos x = \theta\), alors un autre angle qui a le même cosinus peut-être obtenu par \(2\pi - \theta\).
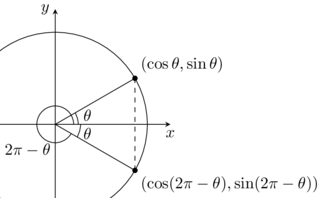
Figure .: Deux angles avec le même cosinus.
Deux angles avec le même sinus
Les deux angles entre 0 et \(2\pi\) qui donnent le même sinus ont la même coordonnée en \(y\). Par conséquent, si \(\arcsin y = \theta\), alors un autre angle qui a le même sinus peut-être obtenu par \(\pi - \theta\).
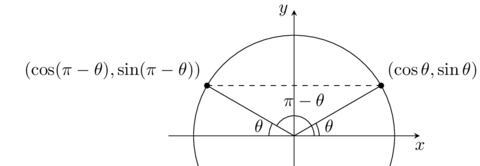
Figure .: Deux angles avec le même sinus.
Deux angles avec la même tangente
Les deux angles entre 0 et \(2\pi\) qui donnent la même tangente ont le même rapport des coordonnées en \(x\) et en \(y\). Par conséquent, si \(\arctan z = \theta\), alors un autre angle qui a la même tangente peut-être obtenu par \(\pi + \theta\).
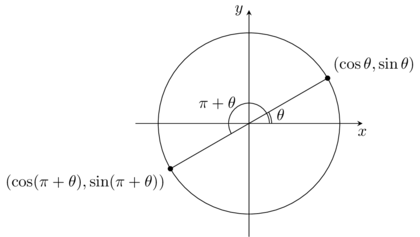
Figure .: Deux angles avec la même tangente.
Exercices
En classe, nous travaillerons sur les exercices des diapositives suivantes