1 Oscillations

Exercices

En classe, nous travaillerons sur les exercices des diapositives suivantes.

1.1 Résumé des définitions

Mouvement harmonique simple (MHS)

Mouvement de va et vient autour d’une position d’équilibre causé par une force dont la grandeur est proportionnelle à la distance par rapport au point d’équilibre et la direction est toujours vers le point d’équilibre. La position en fonction du temps est décrite par une fonction sinusoïdale, par exemple : \[\begin{equation} x = x_m \cos(\omega t + \phi). \tag{1.1} \end{equation}\]

Amplitude

Distance maximale entre la position d’équilibre et l’objet en mouvement harmonique simple. Elle est représentée par \(x_m\) dans l’équation (1.1).

Phase

Argument de la fonction sinusoïdale qui décrit un mouvement harmonique simple, i.e. : \(\omega t + \phi\) dans l’équation (1.1).

Constante de phase

Constante dont la valeur est fixée par les conditions initiales du mouvement harmonique simple. Elle est représentée par \(\phi\) dans l’équation (1.1).

Fréquence angulaire

Nombre de radians par lequel la phase d’un mouvement harmonique simple augmente chaque unité de temps. Elle est représentée par \(\omega\) dans l’équation (1.1).

Fréquence

Nombre d’aller-retour qu’un objet en mouvement harmonique simple effectue par unité de temps. La fréquence \(f\) est reliée à la fréquence angulaire par \[f = \frac{\omega}{2\pi}\] puisque un aller-retour correspond à une variation de phase de \(2\pi\) radians.

Période

Durée d’un aller-retour dans un mouvement harmonique simple. La période, \(T\), est l’inverse de la fréquence donc \[T = \frac{1}{f} = \frac{2\pi}{\omega}.\]

1.2 Évolution temporelle d’un MHS

\(x(t) =\) \(\cos(\) \(t +\) \()\)

\(v_x(t) = -\) \(\sin(\) \(t +\) \()\)

\(a_x(t) = -\) \(\cos(\) \(t +\) \()\)

\(x_m\)
\(\omega\)
\(\phi\)

1.3 Système bloc-ressort

Dans le cas d’un système composé d’un bloc de masse \(m\) et d’un ressort dont la constante de rappel est \(k\), la fréquence angulaire des oscillations du bloc est donnée par \[\omega = \sqrt{\frac{k}{m}}.\]

1.4 Énergie dans un système bloc ressort

Le graphique suivant montre comment l’énergie potentielle et l’énergie cinétique varient selon la position du bloc.

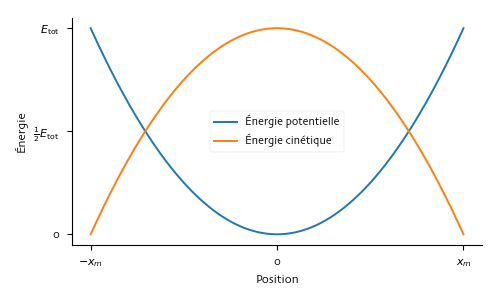
Énergie en fonction de la position

La variation d’énergie potentielle et d’énergie cinétique est deux fois plus rapide que la variation de position. C’est ce qui est illustré dans les graphiques suivants.

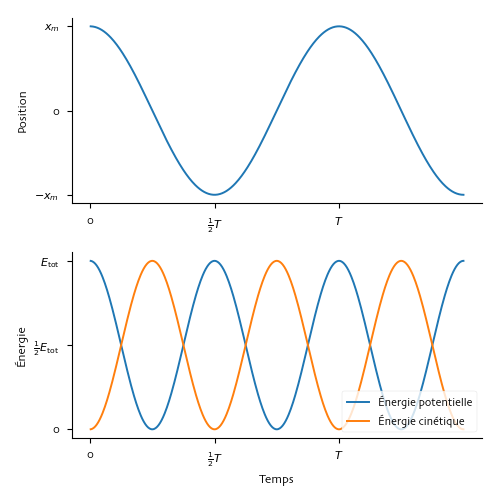
Position et énergie en fonction du temps