Toute la psychopop moderne nous encourage à mieux nous connaître. On nous rabâche les oreilles avec Socrate : «Connais-toi toi-même». Je pense me connaitre assez bien. Il y a cependant une chose à mon sujet que j’ignore encore : mon volume. Alors ce soir, plutôt que de regarder des séries en rafale sur Netflix, j’ai décidé de remédier à cette lacune importante. Et après avoir lu cet article, vous pourrez en faire de même!
Selon Wolfram Alpha, le volume moyen d’un corps humain adulte est de 66.4 L. Ceux qui me connaissent savent que je suis plutôt mince, donc il semble raisonnable de supposer que mon volume doit être légèrement plus faible que la moyenne. La seule façon d’en être sûr, c’est de faire la mesure.
Méthode expérimentale
Pour mesurer le volume d’un objet irrégulier comme un corps humain, la façon la plus simple est d’utiliser la méthode par déplacement d’eau. On plonge l’objet dans un contenant d’eau et on mesure le volume d’eau déplacé. Si l’objet est complètement submergé, le volume déplacé est égal au volume de l’objet.
Le contenant que j’utiliserai est ma baignoire. Elle est suffisamment grande pour que je puisse y entrer et, avec un peu de chance, réussir à m’y submerger complètement. Ma baignoire a une forme semblable à un prisme dont la base est un rectangle arrondi. Les parois sont presque verticales, et pour simplifier l’analyse, j’ignorerai le faible angle qu’elles font avec la verticale.
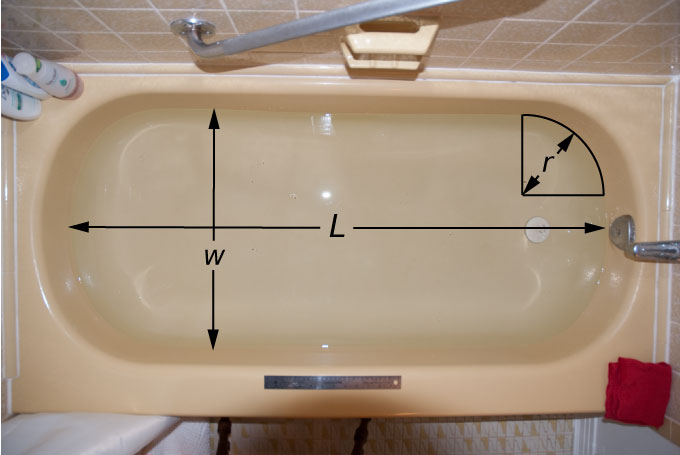
La surface de l’eau dans la baignoire peut-être déterminée à partir de la longueur \(L\), la largeur \(w\) et le rayon des coins arrondi \(r\). Le plus simple est de calculer l’aire du grand rectangle \(Lw\) puis de soustraire les coins. Si on place les quatre coins ensemble, on obtient un cercle de rayon \(r\) inscrit dans un carré \( 2r \times 2r\). L’aire à soustraire est donc l’aire du carré moins celle du cercle soit \[4r^2 - \pi r^2 = (4 - \pi) r^2\] (cette surface est illustrée par la zone hachurée dans la figure ci-dessous).
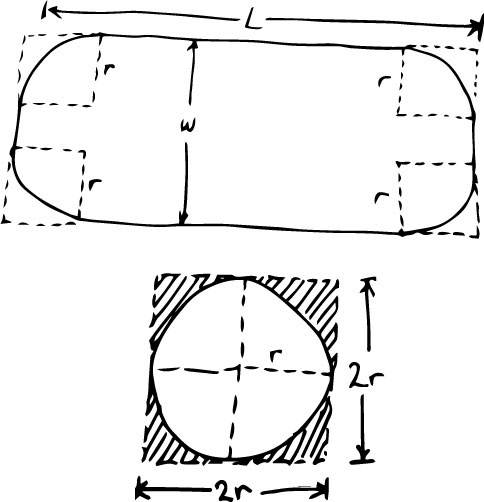
L’aire de la surface d’eau est donc \[S = Lw - (4 - \pi)r^2.\]
J’ai fixé une règle en acier inoxydable sur le côté de la baignoire avec du ruban adhésif. Pour que le ruban tienne bien, il est préférable de bien assécher la paroi de la baignoire avec une serviette sèche. Une des extrémités de la règle se trouve sous la surface de l’eau.

En faisant une lecture \(x_0\) sur la règle avant que je n’entre dans l’eau et une lecture \(x_1\) lorsque je serai complètement submergé, on peut obtenir le changement de hauteur de la surface d’eau \[\Delta h = x_1 - x_0.\] En multipliant ce changement de hauteur par l’aire \(S\), on trouve le volume d’eau déplacé, et donc le volume de mon corps \[V = S\Delta h.\]
Pour garder une trace des lectures effectuées (et pour pouvoir faire une lecture lorsque je serai complètement submergé dans l’eau), j’ai installé ma caméra sur un trépied à côté de la baignoire. La caméra est orientée pour prendre une photo du niveau de l’eau sur la règle. Il va sans dire que caméra numérique et baignoire pleine d’eau ne font pas nécessairement bon ménage. Si vous tentez l’expérience, prenez les précautions nécessaires pour ne pas que votre caméra se retrouve dans l’eau. Je décline toute responsabilité pour le bris d’équipement résultant de la réalisation de cette expérience.
Résultats
Les dimensions de la baignoire se trouve dans le tableau ci-dessous. Les mesures ont été prises avec un ruban à mesurer Johnson Auto-Lock 3.5 m gradué au millimètre. La largeur et la longueur de la baignoire varient selon l’endroit où la mesure est effectuée. En prenant les mesures à plusieurs endroits, j’ai déterminé qu’il y avait une variation de l’ordre de 5 mm. Les incertitudes sur \(L\) et \(w\) sont obtenues en ajoutant ce 5mm à l’incertitude de l’instrument qui est de 1 mm.
J’ai mesuré le rayon en plaçant le ruban à mesurer à l’endroit approximatif où se trouve le centre du cercle. S’il est possible de pivoter le ruban autour de ce point de telle sorte que l’extrémité du ruban demeure en contact avec la paroi de la baignoire, le bon rayon a été trouvé. J’ai effectué cette mesure à main levée et il était à peu près impossible de maintenir une extrémité du ruban complètement fixe lors de la rotation ce qui explique l’incertitude élevée pour cette mesure. Cette incertitude permet aussi de tenir compte du fait que les coins de la baignoire ne sont pas parfaitement circulaires.
| L | w | r |
| cm | cm | cm |
| 136.5 ± 0.6 | 59.0 ± 0.6 | 21 ± 1 |
À partir de ces mesures, on obtient une surface de \(S = (76.4 ± 1.6)\; \mathrm{dm}^2\).
J’ai mesuré le niveau de l’eau sans que je ne sois dans la baignoire avant d’y entrer pour la première fois et après en être sorti à la fin de l’expérience. Cela me permet de tenir compte d’éventuelles fuites d’eau par le bouchon ou par le trop-plein, et de l’évaporation. L’image ci-dessous montre que les deux mesures sont pratiquement identiques. Il n’y a donc pas eu de changement significatif du volume d’eau au cours de l’expérience.

Lorsque je suis entré dans la baignoire, je me suis rapidement aperçu que je n’arriverais jamais à me submerger complètement. La baignoire est trop petite pour moi. J’ai donc opté pour une méthode légèrement plus complexe et incertaine. J’ai mesuré le niveau d’eau lorsque tout mon corps sauf une jambe était submergé, \(x_{11}\), et j’ai repris une mesure lorsque tout mon corps sauf mes deux jambes était submergé, \(x_{12}\). L’idée c’est que je pourrai mesurer le volume de «Loïc moins une jambe» \(V_1\) et le volume de «Loïc moins deux jambes» \(V_2\). En calculant \(2V_1 - V_2\) j’obtiens «Deux Loïc moins deux jambes» moins «Loïc moins deux jambes» ce qui donne évidemment, «Loïc». En prime, je peux aussi calculer \(V_1 - V_2\) pour obtenir le volume d’une de mes jambes. Bon, je sais, tout ça est un peu morbide, mais ça marche!
Il y a beaucoup de choses qui peuvent mal tourner lorsque je suis dans l’eau. D’une part, il est assez difficile de rester complètement submergé avec une jambe en l’air. D’autre part, en essayant de me submerger, je fais bouger la surface de l’eau et le niveau indiqué sur la règle au moment où la photo est prise n’est probablement par le bon. Enfin, j’essayais de vider mes poumons le plus possible pour m’aider à rester sous l’eau, mais des variations dans la quantité d’air qu’il restait dans mes poumons peuvent affecter le volume total de mon corps. Pour pallier à ces problèmes, j’ai répété chaque mesure deux fois. Je l’aurais fait plus souvent si ce n’était du fait que la position recroquevillée pour entrer dans la baignoire était vraiment inconfortable.

Les images ci-dessus montrent les quatre mesures effectuées. Étonnamment, les deux essais donnent pratiquement les mêmes résultats. Par contre, la réflexion et la réfraction de la lumière de même que la présence d’un ménisque rendent difficile la détermination de la position du niveau de l’eau sur la règle. Par conséquent, j’ai décidé d’ajouter une incertitude de 0.5 mm à l’incertitude de 0.5 mm due à l’instrument.
| x0 | x11 | x12 |
| cm | cm | cm |
| 4.7 ± 0.1 | 12.0 ± 0.1 | 10.9 ± 0.1 |
Analyse et conclusion
Enfin, voici le moment de vérité. À partir des données brutes décrites dans la section précédente, il ne reste qu’à calculer \(V_1\), \(V_2\) et finalement mon volume. Je calcule chacun de ces volumes à partir du changement de hauteur avec une jambe hors de l’eau \(\Delta h_1\) et avec deux jambes hors de l’eau \(\Delta h_2\).
| S | Δh1 | Δh2 | V1 | V2 |
| dm2 | dm | dm | L | L |
| 76.4 ± 1.6 | 0.73 ± 0.02 | 0.62 ± 0.02 | 56 ± 3 | 47 ± 2 |
Le volume d’une de mes jambes est donc de \[V_\mathrm{jambe} = V_1 - V_2 = (8 ± 5)\; \mathrm{L},\] et mon volume est \[V = 2V_1 - V_2 = (64 ± 8)\; \mathrm{L}.\] Il semble donc que mon volume soit tout à fait dans la moyenne. Je reste persuadé que mon volume est plus petit que la moyenne, mais pour le prouver je devrais refaire l’expérience en prenant soin de diminuer l’incertitude sur les mesures.
L’incertitude sur le résultat final serait environ deux fois plus petite si j’avais été capable d’entrer complètement sous l’eau sans avoir à mettre les jambes en l’air. Une baignoire légèrement plus grande m’aurait donc permis de diminuer l’incertitude de moitié. Une autre façon d’obtenir un résultat plus précis serait de mieux calibrer mon «instrument». Plutôt que d’essayer de mesurer l’aire de la surface d’eau, je pourrais ajouter un volume d’eau connu (et mesuré assez précisément) et voir quelle est l’augmentation de la hauteur de l’eau. Pour améliorer les lectures du niveau de l’eau, il faudrait placer l’appareil photo un peu plus proche de la règle ou utiliser un objectif avec une plus grande longueur focale. Un flash indirect pourrait aussi aider à diminuer les reflets sur l’eau et donc rendre la mesure plus claire.
Je vous souhaite la meilleure des chances pour essayer de mesurer votre propre volume! Si une idée brillante vous vient à l’esprit pour améliorer l’expérience, vous pouvez m’en informer sur Twitter.