Aux étudiants qui apprennent les méthodes d’analyse communes en science expérimentale, on mentionne souvent que la qualité d’un modèle linéaire correspond à la valeur du coefficient de détermination \(R^2\). Plus le coefficient est proche de un, meilleur est le modèle pour représenter fidèlement les données. Ces étudiants n’ont, en général, pas de formation en statistiques et le contexte d’un cours de science expérimentale (physique, chimie ou biologie) ne donne pas l’occasion de décrire en détail le calcul qui permet d’obtenir \(R^2\). Ils ne retiennent donc qu’un concept assez vague qui se résume à « \(R^2\) proche de un \(\Rightarrow\) bon modèle ». Or, cette conclusion est très souvent incorrecte et le coefficient de détermination n’est qu’un indice parmi de nombreux autres qui permettent de valider un modèle.
Le problème devient encore plus évident lorsque les étudiants découvrent les différents types de courbes de tendance que les logiciels d’analyse tel qu’Excel permettent de calculer. Si un étudiant calcule une courbe de tendance polynomiale de degré suffisamment élevé, il obtient un coefficient de détermination égal à un et s’exclame alors « Eurêka! » alors qu’en réalité il ne vient que de trouver un modèle extrêmement complexe qui n’a aucune base scientifique pour expliquer le phénomène observé.
Dans ce qui suit, nous explorerons un exemple typique de modèle inapproprié et nous verrons pourquoi il est toujours possible de trouver un polynôme qui passe par tous les points expérimentaux.
Déterminer la force exercée par un arc
Imaginez qu’on vous donne comme mission de déterminer le module de la force exercée par la corde d’un arc sur une flèche pour différentes élongations. Vous allez au laboratoire et, à l’aide d’un dynamomètre, vous tirez sur la corde de l’arc pour atteindre l’élongation désirée. Vous mesurez le module de la force indiqué sur le dynamomètre et vous répétez la procédure pour différentes élongations. Si vous avez les ressources pour faire l’expérience, allez-y maintenant et revenez avec vos données. Sinon, considérez les données ci-dessous que j’ai recueillies moi-même.
| Élongation (m) | Module de la force (N) |
|---|---|
| 0,040(2) | 17(1) |
| 0,120(3) | 32(1) |
| 0,200(4) | 55(1) |
| 0,280(4) | 73(1) |
(Le chiffre entre parenthèse indique l’incertitude sur la dernière décimale affichée.)
Le graphique ci-dessous montre la relation entre l’élongation et la force.
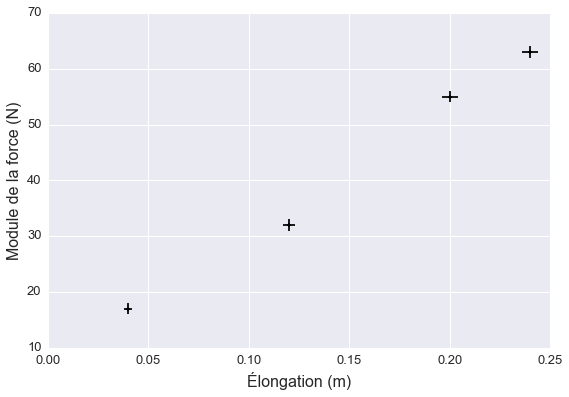
La relation semble à peu près linéaire, ce qui concorde avec l’hypothèse que l’arc se comporte comme un ressort idéal régi par la loi de Hooke :
$$ F = kS $$
où \(F\) est le module de la force exercée par l’arc, \(k\) est la constante de rappel et \(S\) est l’élongation. Reste à déterminer si ce modèle est le plus approprié.
Comparaison de différents modèles
Vous utilisez ensuite votre logiciel d’analyse de données favori pour tester différents modèles. Par exemple, vous pouvez essayer un modèle linéaire, quadratique ou cubique. Excel rend ce genre de tests extrêmement facile. Vous pouvez simplement ajouter des courbes de tendance à partir d’un menu et faire afficher le coefficient de détermination sur le graphique. Le graphique ci-dessous montre les données et les trois modèles.
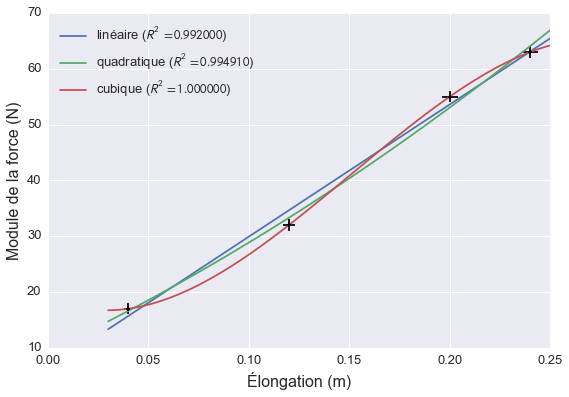
Si on ne se fie qu’au coefficient de détermination, le modèle cubique est le meilleur alors que le modèle linéaire est le moins approprié. Le modèle cubique passe en effet par chacun des points et semble donc décrire très exactement ce qui se passe.
Par contre, il n’y a aucune raison physique qui justifie un modèle cubique alors que le modèle linéaire correspond à une loi empirique bien connue. Peut-être que l’arc ne se comporte par comme un ressort idéal et que différents phénomènes expliquent la pertinence d’une loi cubique. Pour le savoir, rien de mieux que d’amasser plus de données!
| Élongation (m) | Module de la force (N) |
|---|---|
| 0,040(2) | 17(1) |
| 0,060(3) | 23(1) |
| 0,080(3) | 27(1) |
| 0,120(3) | 32(1) |
| 0,160(3) | 46(1) |
| 0,200(4) | 55(1) |
| 0,240(4) | 63(1) |
| 0,280(4) | 73(1) |
| 0,320(4) | 80(2) |
Un graphique de ces données avec les trois modèles élaborés jusqu’ici montre clairement lequel est le plus approprié.
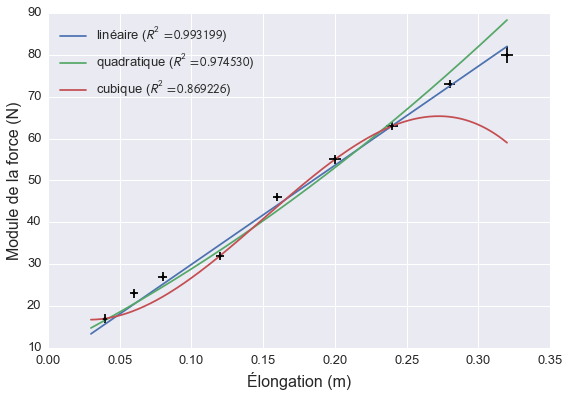
On voit clairement que ni le modèle cubique ni le modèle quadratique n’arrivent à expliquer les nouvelles données et ce, même si leur coefficient de détermination lorsque nous avons construit le modèle était supérieur à celui du modèle linéaire. Dans le domaine de l’apprentissage-machine, ce phénomène est appelé du sur-apprentissage (overfitting en anglais). En réalité, l’arc se comporte presque comme un ressort idéal et le modèle linéaire est le meilleur modèle pour expliquer son comportement.
Le modèle linéaire a aussi l’avantage d’être plus simple que les deux autres. Plus un modèle est complexe, plus il suivra de près les données, mais moins il sera facile à expliquer physiquement.
Construire un polynôme qui passe par un ensemble de points
Nous allons maintenant voir comment, pour tout ensemble de données, nous pouvons construire un modèle polynomial qui passera par tous les points et qui aura donc un coefficient de détermination de 1.
Si nous avons \(N\) points \((x_i, y_i)\), il est toujours possible de trouver un polynôme \(p\) de degré au plus \(N - 1\) qui passe par chacun des points. Ce polynôme est assez simple à construire. Il doit satisfaire
$$p(x_1) = y_1 \\ p(x_2) = y_2 \\ \vdots \\ p(x_N) = y_N$$
Nous pouvons satisfaire la première égalité facilement avec \(p(x) = y_1\). Évidemment, ce polynôme ne satisfait aucune des autres égalités. Si nous voulons satisfaire la deuxième égalité, nous pouvons ajouter un terme \(y_2\) et multiplier le premier terme par \(x_2 - x\) de telle sorte que lorsqu’on évalue le polynôme à \(x = x_2\), le premier terme disparaît et il ne reste que le second.
$$p(x) = y_1 (x_2 - x) + y_2$$
Malheureusement, cette version ne satisfait plus la première égalité car \(p(x_1) = y_1 (x_2 - x_1) + y_2\). Nous rétablissons assez facilement la situation en multipliant le second terme par \(x_1 - x\) et en divisant le premier terme par \(x_2 - x_1\). Nous obtenons alors le polynôme
$$p(x) = y_1 \frac{x_2 - x}{x_2 - x_1} + y_2 (x_1 - x).$$
Ce polynôme vaut \(y_1\) à \(x_1\) mais il vaut maintenant \(y_2 (x_1 - x_2)\) à \(x_2\). Si nous divisons le deuxième terme par \(x_1 - x_2\), nous obtenons un polynôme qui satisfait les deux premières égalités :
$$p(x) = y_1 \frac{x_2 - x}{x_2 - x_1} + y_2 \frac{x_1 - x}{x_1 - x_2}.$$
Ce polynôme est linéaire (degré 1) et passe par deux points de données.
En continuant le raisonnement de la sorte, nous arrivons à construire le polynôme suivant qui satisfait les \(N\) égalités :
$$p(x) = \sum_{i = 1}^N y_i \frac{\Pi_{j = 1\\j \neq i}^N (x_j - x)}{\Pi_{j = 1\\j \neq i}^N (x_j - x_i)}.$$
(Exercice : Vérifiez que \(p(x_i) = y_i\) pour \(i = 1, \ldots, N\).)
Le degré de ce polynôme est déterminé par le numérateur de ses termes. Puisque le numérateur de chaque terme contient \(N - 1\) facteurs (\(j\) va de \(1\) jusqu’à \(N\), mais saute par-dessus la valeur \(i\)), le polynôme est donc de degré au plus \(N - 1\). Ce polynôme s’appelle un polynôme d’interpolation de Lagrange.
La construction du polynôme d’interpolation de Lagrange montre que pour n’importe quel ensemble de \(N\) points, il est possible de trouver un polynôme qui passe par tous ces points et que ce polynôme a un degré au plus \(N - 1\).
Interpolation de Lagrange pour l’arc
Le calcul du polynôme d’interpolation de Lagrange pour les données que nous
avons recueillies sur la force exercée par l’arc est directe, mais un peu
fastidieuse. Heureusement, scipy contient une fonction lagrange qui peut
faire le travail pour nous.
import numpy as np from scipy.interpolate import lagrange elongation = np.array([4.0, 12.0, 20.0, 24.0]) / 100.0 force = np.array([ 17.0, 32.0, 55.0, 63.0]) lagpoly = lagrange(elongation, force) print(lagpoly)
$$-6771 x^3 + 3062 x^2 - 161.7 x + 19$$
Nous pouvons calculer la courbe de tendance polynomiale de degré 3 par la
méthode des moindres carrés en utilisant la fonction polyfit dans numpy
(c’est la courbe de tendance qui se trouve dans les graphiques ci-dessus).
model = np.poly1d(np.polyfit(elongation, force, 3)) print(model)
$$-6771 x^3 + 3062 x^2 - 161.7 x + 19$$
Le polynôme de degré 3 obtenu par la méthode des moindres carrés est donc le polynôme d’interpolation de Lagrange. Sachant que ce polynôme passe exactement par tous les points, il n’est pas surprenant que le coefficient de détermination obtenu soit égal à 1.
Conclusion
Comme tout ensemble de données admet un polynôme d’interpolation de Lagrange, il est certain qu’il est possible d’obtenir un modèle avec un coefficient de détermination de 1. Cela ne veut pas dire que le modèle est une description adéquate des données : il est possible que nous soyons victime de sur-apprentissage.
Un coefficient de détermination très près de 1 ne correspond donc pas nécessairement à un bon modèle. Le coefficient de détermination est une valeur utile pour juger de la qualité d’un modèle, mais elle doit être utilisée en conjonction avec d’autres critères pour arriver à une conclusion raisonnable.