Introduction
En discutant avec ma douce moitié à propos du fait que beaucoup de nos connaissances ont une date d’anniversaire au printemps, j’en suis venu à m’interroger sur la distribution des naissances au cours d’une année. Si une personne est choisie au hasard, est-ce que la probabilité que cette personne soit née en janvier est 1/12 ? Et en février ?
En fouillant un peu, je me suis aperçu que ce n’est pas le cas. La variation saisonnière des naissances est un phénomène bien connu des démographes depuis longtemps (voir, par exemple, Udry et Morris (1967), Menken (1979), Bobak et Gjonca (2001)). Sans se lancer dans les théories sociologiques qui tentent d’expliquer le phénomène, nous pouvons l’observer facilement à partir de données disponibles sur le site de Statistique Canada. L’exercice est en même temps un petit tutoriel sur l’utilisation de R pour l’analyse et la visualisation de données.
Si vous lisez jusqu’à la toute fin, vous aurez droit à un truc infaillible pour devenir riche.
Collecte et nettoyage
La première chose à faire est de télécharger les données à partir de la
table 102-4502 du site de Statistique Canada.
Pour télécharger le fichier, le décompresser et le charger dans un
data.frame, il suffit de deux commandes dans R.
download.file( "http://www20.statcan.gc.ca/tables-tableaux/cansim/csv/01024502-eng.zip", dest = "01024502-eng.csv.zip") rawdata = read.csv(unzip("01024502-eng.csv.zip"), strip.white = TRUE)
Il est important de noter que j’ai utilisé le fichier anglais. Je ne l’ai pas vérifié, mais je suppose que la version française des mêmes données contient du texte français qui ne pourra pas être traité par les commandes suivantes.
Extraction des données pertinentes
Le fichier contient le nombre de naissances dans chaque province pour chacun
des mois de l’année, de 1991 à 2011. Il contient également des données
combinées pour l’ensemble du Canada et pour chaque année. Les données sont
brutes : il n’est pas simple d’extraire les lignes appropriées parce que la
sélection doit se faire selon les chaînes de caractères contenues dans ces
lignes. Avant de se lancer dans le nettoyage, il est plus sage de d’abord
observer ce que nous avons entre les mains. Les colonnes sont obtenues par
la commande names :
names(rawdata)
## [1] "Ref_Date" "GEO" "MONTHBIRTH" "UNIT" "Value"
Pour avoir un aperçu des données elles-mêmes, il suffit d’extraire quelques lignes :
rawdata[1:5, ]
## Ref_Date GEO MONTHBIRTH ## 1 1991 Canada, place of residence of mother Total, month of birth ## 2 1992 Canada, place of residence of mother Total, month of birth ## 3 1993 Canada, place of residence of mother Total, month of birth ## 4 1994 Canada, place of residence of mother Total, month of birth ## 5 1995 Canada, place of residence of mother Total, month of birth ## UNIT Value ## 1 Number of live births 402533 ## 2 Number of live births 398643 ## 3 Number of live births 388394 ## 4 Number of live births 385114 ## 5 Number of live births 378016
La présence de longues descriptions comme Canada, place of residence of
mother et Total, month of birth complique un peu les choses. La fonction
read.csv définit automatiquement des facteurs pour toutes les colonnes qui
contiennent des chaînes de caractères, nous pouvons donc obtenir facilement la
liste des niveaux de chaque colonne.
levels(rawdata$GEO)
## [1] "Alberta, place of residence of mother" ## [2] "British Columbia, place of residence of mother" ## [3] "Canada, place of residence of mother" ## [4] "Manitoba, place of residence of mother" ## [5] "New Brunswick, place of residence of mother" ## [6] "Newfoundland and Labrador, place of residence of mother" ## [7] "Northwest Territories including Nunavut, place of residence of mother" ## [8] "Northwest Territories, place of residence of mother" ## [9] "Nova Scotia, place of residence of mother" ## [10] "Nunavut, place of residence of mother" ## [11] "Ontario, place of residence of mother" ## [12] "Prince Edward Island, place of residence of mother" ## [13] "Quebec, place of residence of mother" ## [14] "Saskatchewan, place of residence of mother" ## [15] "Unknown province or territory, place of residence of mother" ## [16] "Yukon, place of residence of mother"
levels(rawdata$MONTHBIRTH)
## [1] "Month of birth, April" "Month of birth, August" ## [3] "Month of birth, December" "Month of birth, February" ## [5] "Month of birth, January" "Month of birth, July" ## [7] "Month of birth, June" "Month of birth, March" ## [9] "Month of birth, May" "Month of birth, November" ## [11] "Month of birth, October" "Month of birth, September" ## [13] "Total, month of birth"
levels(rawdata$UNIT)
## [1] "Number of live births" "Percentage of live births"
Pour garder les choses simples, contentons-nous d’analyser les données pour
l’ensemble du Canada. Nous utiliserons les fréquences de naissances mensuelles
pour calculer les fréquence relatives. Par conséquent, seules les lignes
contenant la chaîne de caractère Canada, place of residence of mother dans la
colonne GEO et Number of live births dans la colonne MONTHBIRTH seront
conservées.
La fonction grepl peut être utilisée pour éliminer toutes les lignes du
tableau de données qui ne décrivent pas l’ensemble du Canada avec des nombres
absolus pour chaque mois. grepl prend une expression régulière comme premier
argument et une liste (ou un élément unique) comme second argument. La
fonction retourne une liste de valeurs booléennes qui indique si l’expression
régulière a été trouvée à chacune des positions de la liste d’entrée. Par
exemple,
grepl("bon", c("bonjour", "allo"))
## [1] TRUE FALSE
La commande suivante sélectionne toutes les lignes pour lesquelles la colonne
GEO commence par Canada, la colonne UNIT commence par Number et la
colonne MONTHBIRTH commence par Month. De plus, seules les colonnes
d’intérêt sont retenues.
canada.births = rawdata[grepl("^Canada", rawdata$GEO) & grepl("^Number", rawdata$UNIT) & grepl("^Month", rawdata$MONTHBIRTH), c("Ref_Date", "MONTHBIRTH", "Value")]
Le même résultat peut aussi être obtenu avec la commande subset :
canada.births = subset(rawdata, grepl("^Canada", GEO) & grepl("^Number", UNIT) & grepl("^Month", MONTHBIRTH), select = c(Ref_Date, MONTHBIRTH, Value))
Ensuite, nous renommons chaque colonne avec un nom plus descriptif.
names(canada.births) = c("Year", "Month", "Births")
Réorganisation des facteurs
On peut simplifier le tableau en éliminant Month of birth, pour n’utiliser
que le nom du mois. Encore une fois, les expressions régulières sont parfaites
pour cette tâche. La fonction gsub remplace toutes les occurrences d’une
expression régulière dans une liste. Si l’expression à trouver contient des
groupes (dénotés par des parenthèses), ces groupes peuvent être utilisés dans
l’expression de remplacement avec \\1 à \\9.
levels(canada.births$Month) = gsub("Month of birth, ([a-zA-Z].)", "\\1", levels(canada.births$Month)) head(canada.births)
## Year Month Births ## 43 1991 January 32150 ## 44 1992 January 31974 ## 45 1993 January 30989 ## 46 1994 January 30265 ## 47 1995 January 29975 ## 48 1996 January 29410
Dans le tableau de données, les mois sont des niveaux, mais R ne sait pas comment ordonner ces niveaux. Par défaut, les niveaux décrits par des chaînes de caractères sont ordonnés alphabétiquement. La commande suivante place les mois en ordre chronologique.
canada.births$Month = factor(canada.births$Month, levels = c("January", "February", "March", "April", "May", "June", "July", "August", "September", "October", "November", "December"))
Ces données forment une série temporelle et R possède justement une classe pour
ce type de données. Pour l’utiliser, il faut d’abord réorganiser les lignes de
canada.births en ordre chronologique.
canada.births = canada.births[with(canada.births, order(Year, Month)), ] head(canada.births)
## Year Month Births ## 43 1991 January 32150 ## 85 1991 February 30259 ## 127 1991 March 34782 ## 169 1991 April 35314 ## 211 1991 May 36272 ## 253 1991 June 34275
Calcul des fréquences relatives
Avant de créer des séries temporelles, un petit calcul risque d’être fort utile. Le nombre total de naissances varie probablement d’année en année et même si c’est un phénomène intéressant, ce n’est pas celui que nous étudions en ce moment. Pour éliminer l’effet des variations annuelles, il suffit de calculer le pourcentage des naissances de l’année qui ont lieu chaque mois. Voici deux façons de faire ce calcul.
La fonction aggregate permet de combiner les données d’une colonne selon la
valeur d’une autre colonne en utilisant une fonction spécifique. Pour obtenir
le nombre total de naissances chaque année nous regroupons les éléments de la
colonne Births par Year avec la fonction somme. Chaque élément est ensuite
répété 12 fois pour obtenir une liste de la même longueur que l’originale. Il
ne reste qu’à ajouter la colonne désirée.
births_per_year = aggregate(Births ~ Year, data = canada.births, FUN = sum) relbirths = canada.births relbirths$RelBirths = relbirths$Births/rep(births_per_year$Births, each = 12) head(relbirths)
## Year Month Births RelBirths ## 43 1991 January 32150 0.07987 ## 85 1991 February 30259 0.07517 ## 127 1991 March 34782 0.08641 ## 169 1991 April 35314 0.08773 ## 211 1991 May 36272 0.09011 ## 253 1991 June 34275 0.08515
La deuxième façon de procéder est plus directe mais nécessite un paquetage
additionnel, data.table.
library(data.table) birthstable = data.table(canada.births) birthstable = birthstable[, `:=`(RelBirths, Births/sum(Births)), by = Year] head(birthstable)
## Year Month Births RelBirths ## 1: 1991 January 32150 0.07987 ## 2: 1991 February 30259 0.07517 ## 3: 1991 March 34782 0.08641 ## 4: 1991 April 35314 0.08773 ## 5: 1991 May 36272 0.09011 ## 6: 1991 June 34275 0.08515
Création de séries temporelles
Nous créons deux séries temporelles : une avec le nombre de naissances et l’autre avec les fréquences relatives.
births.ts = ts(data = relbirths$Births, start = c(1991, 1), frequency = 12) relbirths.ts = ts(data = relbirths$RelBirths, start = c(1991, 1), frequency = 12)
Pour le reste de l’analyse, nous utiliserons les trois objets relbirths,
relbirths.ts et births.ts.
Visualisation des données
R peut tracer un graphique du pourcentage des naissances en fonction du mois de l’année, il combine automatiquement les données de chaque année et produit un graphique en boîtes à moustache (mieux connu en anglais sous le nom de box plot). Le trait pointillé horizontal correspond à 1/12.
plot(RelBirths ~ Month, data = relbirths, xlab = "Mois", ylab = "Pourcentage des naissances annuelles") abline(h = 1/12, lty = 3)
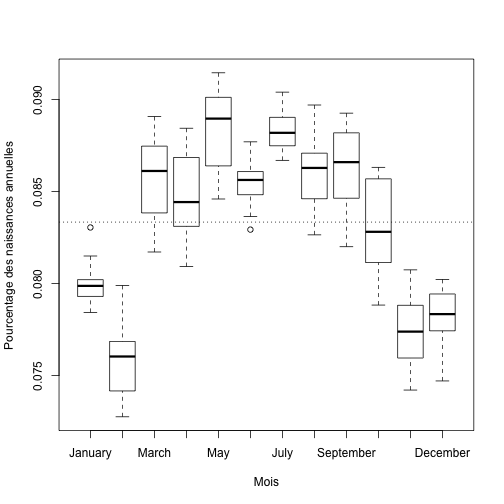
Cette figure montre une variation claire du nombre de naissances au cours de l’année. Les mois de mars à octobre sont les plus achalandés alors que les mois de novembre à février le sont moins. Par exemple, environ 7.6% des naissances ont lieu en février alors que près de 8.8% ont lieu en mai (notons que 1/12 correspond à environ 8.3%).
Les graphiques des séries temporelles sont encore plus intéressants. Le nombre de naissances en fonction du temps montre immédiatement qu’il y a à la fois des variations saisonnières mais aussi des variations d’année en année.
plot.ts(births.ts, xlab = "Temps", ylab = "Nombre de naissances")
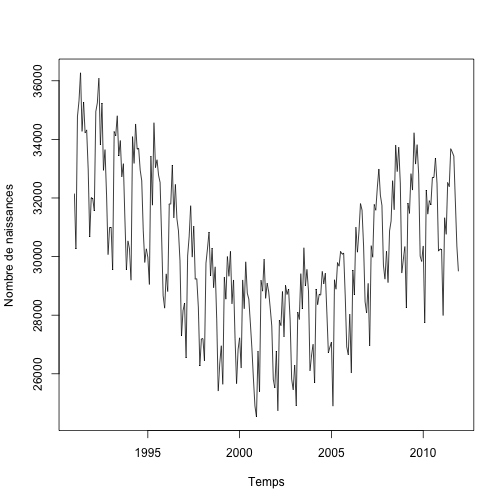
Si nous traçons plutôt les fréquences relatives, l’effet des variations annuelles disparaît et il ne reste que les variations saisonnières.
plot.ts(relbirths.ts, xlab = "Temps", ylab = "Pourcentage des naissances annuelles")
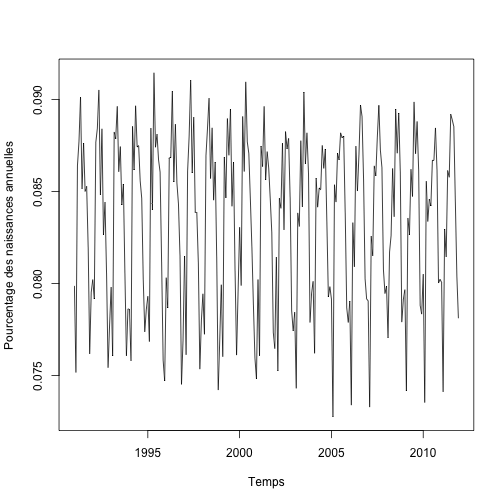
Analyse et modélisation
C’est probablement une déformation professionnelle, mais quand je vois un graphique de série temporelle qui a l’air de celui ci-haut, je pense tout de suite à une faire une analyse de Fourier.
ft = fft(relbirths$RelBirth) nft = length(ft) ft = Mod(c(ft[(nft/2 + 1):nft], ft[1:(nft/2)])) freqs = c(seq(-0.5, 0, length.out = (nft/2)), seq(0, 0.5, length.out = (nft/2))) fftdata = data.frame(freqs, ft)
Voyons à quoi ressemble ce signal dans l’espace des fréquences.
plot(fftdata[130:230, ], t = "l", pch = 20, cex = 0.8, xlab = "Frequence (1/mois)", ylab = "Amplitude") freqmax = freqs[130:230][which.max(ft[130:230])] abline(v = freqmax, lty = 3) text(0.1, 0.63, paste("Frequence:", signif(freqmax, 2), "/ mois"), adj = c(0, 0)) text(0.1, 0.6, paste("Periode", signif(1/freqmax, 2), "mois"), adj = c(0, 0))
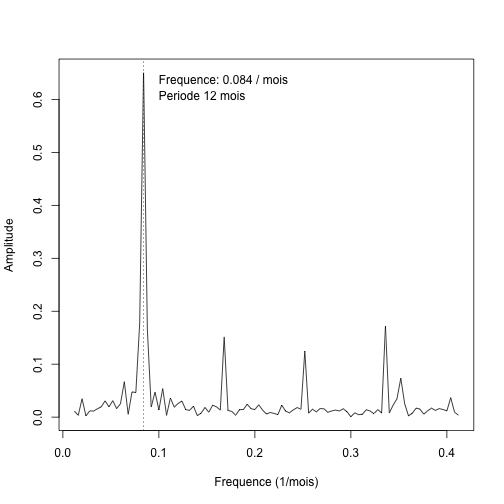
Il y a bel et bien une composante de fréquence 12 mois dans le signal, autrement dit, le pourcentage des naissances peut être modélisé par une fonction sinusoïdale de fréquence \(1 / 12\). R nous permet de trouver cette composante en faisant une régression non linéaire. Pour diminuer le nombre de paramètres (3 au lieu de 4), il est approprié de soustraire la moyenne à la fréquence relative de sorte que le signal soit centré en 0. Comme unité de temps, nous utiliserons le mois.
y = relbirths$RelBirths - 1/12 x = 1:length(y) sine_fit = nls(y ~ A * sin(2 * pi * f * x + k), start = list(A = 0.05, f = 1/12, k = 0)) summary(sine_fit)
## ## Formula: y ~ A * sin(2 * pi * f * x + k) ## ## Parameters: ## Estimate Std. Error t value Pr(>|t|) ## A -5.51e-03 2.19e-04 -25.1 <2e-16 *** ## f 8.26e-02 8.57e-05 963.3 <2e-16 *** ## k 1.93e+00 7.87e-02 24.6 <2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.00245 on 249 degrees of freedom ## ## Number of iterations to convergence: 9 ## Achieved convergence tolerance: 8.41e-07
plot(y ~ x) lines(x, fitted(sine_fit))
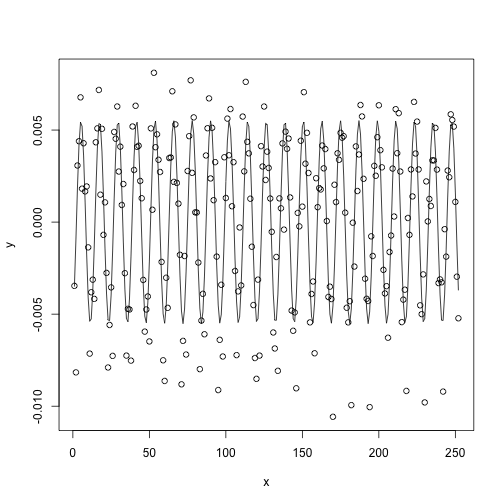
Tous les paramètres du modèle sont statistiquement significatifs. Ainsi donc, on peut utiliser la relation \[ y = -0.00551 \sin(0.519x + 1.93) + 1/12\] pour déterminer le pourcentage des naissances, \(y\), en fonction du mois de l’année, \(x\). Le modèle pourrait être raffiné en y incluant des composantes d’autres fréquences. Comme le montre l’analyse de Fourier des résidus, il reste encore des composantes de périodes bien spécifiques (3 mois étant la suivante). Le reste de la procédure est laissée en exercice… Pour les intéressés, cette procédure est exactement la même que la méthode de blanchissage utilisée en astérosismologie pour déterminer les périodes de pulsation des étoiles (voir, par exemple, Billéres et al. (2000)).
ft = fft(residuals(sine_fit)) nft = length(ft) ft = Mod(c(ft[(nft/2 + 1):nft], ft[1:(nft/2)])) freqs = c(seq(-0.5, 0, length.out = (nft/2)), seq(0, 0.5, length.out = (nft/2))) fftdata = data.frame(freqs, ft) plot(fftdata[130:230, ], t = "l", pch = 20, cex = 0.8, xlab = "Frequence (1/mois)", ylab = "Amplitude") freqmax = freqs[130:230][which.max(ft[130:230])] abline(v = freqmax, lty = 3) text(0.2, 0.16, paste("Frequence:", signif(freqmax, 2), "/ mois"), adj = c(0, 0)) text(0.2, 0.15, paste("Periode", signif(1/freqmax, 2), "mois"), adj = c(0, 0))
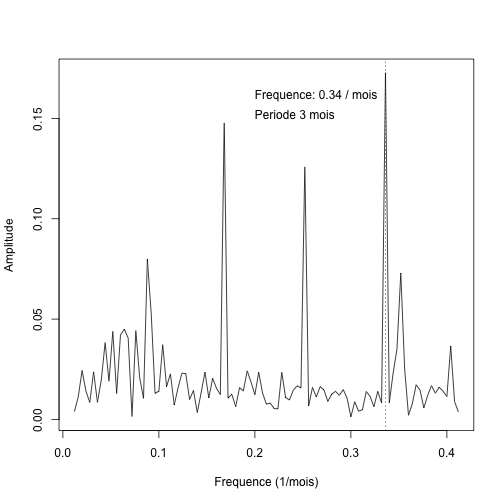
Conclusion
La distribution de probabilité du mois de naissance n’est pas uniforme. Elle suit plutôt une distribution sinusoïdale de période égale à un an. Les mois d’été sont ceux durant lesquels il y a le plus de naissances alors que les mois d’hiver sont ceux durant lesquels il y en a le moins.
Voici donc une idée pour faire de l’argent. Proposez à quelqu’un le jeu suivant. Vous essayer de devinez leur mois d’anniversaire, si vous y arrivez la personne vous donne 10.50$, sinon vous lui donnez 1$. Votre victime, croyant que vous allez choisir un mois au hasard selon une distribution uniforme estimera que l’espérance de son gain est \(-10.50\$ \times 1/12 + 1\$ \times 11/12 = 0.04\$\) et elle sera d’accord pour jouer. De votre côté, vous prédisez le mois de mai à chaque fois que vous jouez. Grâce à l’analyse que nous venons de faire, nous savons que l’espérance de votre gain est \(10.50\$ \times 0.088 - 1\$ \times 0.912 = 0.01\$\). Si vous réussissez à convaincre suffisamment de personnes de jouer, vous deviendrez riche (ou presque).