Sommaire
Une queue est une abstraction mathématique pour représenter une panoplie de situations dans lesquelles des choses arrivent et sont traitées. De quel genre de choses parle-t-on? Et que veulent dire arriver et être traité? Il peut s'agir de clients qui arrivent à la caisse dans une épicerie et qui sont servis par la caissière, de passagers qui se mettent en file pour monter dans un autobus, de documents qui sont empilés dans un classeur en attente d'être signés par un notaire, de paquets qui transitent dans un réseau IP et qui attendent dans un routeur de pouvoir être envoyés à la bonne destination.
Une queue peut être servie par un ou plusieurs serveurs. Par exemple, dans une petite épicerie, il peut n'y avoir qu'une seule caisse. Dans une banque, il y a souvent une queue unique avec plusieurs caissiers : dès qu'un caissier se libère, le prochain client dans la queue se dirige vers cette caisse. Il existe plusieurs types de disciplines dans la queue. Par exemple, la discipline premier arrivé, premier servi est commune à l'épicerie et à l'arrêt d'autobus. La discipline dernier arrivé, premier servi correspond à une boîte de Pringles : le dernier Pringle placé dans la boîte est le premier à être mangé. Dans la discipline continentale, les clients sont pêle-mêle et le prochain client servi est choisi au hasard.
La très grande majorité des queues sont difficiles à étudier théoriquement et il faut souvent utiliser des simulations pour comprendre leur comportement. Par contre, il y a un modèle de queue assez simple, la queue M/M/1, à partir duquel on peut déterminer plusieurs quantités intéressantes comme le temps de service moyen et la longueur moyenne de la queue.
La queue M/M/1 : définitions
Dans une queue M/M/1, les clients arrivent selon un processus de Poisson d'intensité \(\lambda\), c'est-à-dire que le nombre de clients qui arrivent dans un intervalle de temps \(t\), \(N(t)\), est une variable aléatoire de type Poisson et de paramètre \(\lambda t\) :
Pour un processus de Poisson, il est bien connu que le temps entre les arrivées suit une distribution exponentielle de paramètre \(\lambda\). Il n'y a qu'un serveur et le temps pour qu'un client soit servi est distribué selon une loi exponentielle de paramètre \(\mu\).
L'intensité du trafic est défini comme étant le rapport entre le temps de service moyen et le temps moyen entre deux arrivées. Puisque l'espérance d'une variable aléatoire exponentielle est l'inverse de son paramètre, on a que le temps de service, \(T_s \sim \mathrm{Exp}(\mu)\), a
et l'espérance du temps entre deux arrivées, \(T_a \sim \mathrm{Exp}(\lambda)\), est
L'intensité du trafic est donc
L'interprétation intuitive de l'intensité du trafic est simple. Si elle est proche de zéro, le temps entre les arrivées est beaucoup plus grand que le temps de service, par conséquent, la queue sera presque toujours vide et le serveur presque toujours disponible. Si l'intensité du trafic est proche de 1, le temps qu'il faut pour servir un client est à peu près le même que le temps entre les arrivées. En raison des fluctuations aléatoires, la queue peut devenir très longue. Si l'intensité du trafic est supérieure à 1, la queue va croître indéfiniment. Cette intuition sera confirmée par l'analyse plus rigoureuse un peu plus tard.
Dans le modèle que nous allons étudier, tous les clients qui arrivent se placent dans la queue et y demeurent jusqu'à ce qu'ils soient servis. Ce type de modèle ne tient donc pas compte des clients qui quittent la queue si le temps d'attente est trop long ou de ceux qui décident de ne pas s'y joindre parce qu'elle est trop longue.
Les trois éléments de la notation M/M/1 (dite notation de Kendall) décrivent les arrivées, le temps de service et le nombre de serveurs. Le premier M signifie que les arrivées sont Markoviennes, c'est-à-dire que le temps entre les arrivées et exponentiel. Le second M signifie que le temps de service est markovien. Le 1 correspond au fait qu'il n'y a qu'un serveur. Il existe de nombreuses autres queues : M/M/c, M/D/c, G/G/1, etc.
Générateur ou matrice \(Q\)
La longueur de la queue M/M/1 est une chaîne de Markov à temps continu sur les états \(0, 1, 2, \ldots\) Le générateur de cette chaîne est une matrice infinie \(\boldsymbol{\mathrm{G}}\) dont les éléments \(g_{ij}\) sont définis par
dans la limite où \(h\) est très proche de 0. Il est important de noter que le générateur est indépendant du temps parce que la chaîne est homogène, une propriété qui découle de la propriété sans mémoire du processus de Poisson.
Transition de plus d'une unité dans la longueur de la queue
Premier constat important : \(g_{ij} = 0\) si \(i\) et \(j\) diffèrent de plus d'une unité. Pourquoi ? C'est une conséquence de la définition du processus de Poisson : la probabilité qu'il y ait plus d'une arrivée (ou départ) dans un temps \(h\) doit être \(o(h)\), c'est-à-dire que
or, d'après la définition donnée plus haut, la probabilité au numérateur est exactement égale à \(g_{ij}h\). Par conséquent,
ce qui implique que \(g_{ij}\) doit être égal à 0. Le générateur est donc une matrice tridiagonale.
Transition d'une unité dans la longueur de la queue
La chaîne passe de l'état \(i\) à l'état \(i + 1\) s'il y a une arrivée et aucun départ dans l'intervalle \(h\). Comme le temps entre les arrivées et le temps de service sont indépendants, on a
Pour une variable exponentielle \(Y\) de paramètre \(\nu\)
donc,
Puisque \(h\) est petit, on peut développer les exponentielles en série de Maclaurin et ne garder que les deux premiers termes :
L'élément du générateur \(g_{i, i+1}\) est donc simplement \(\lambda\). En inversant le rôle du temps de service et du temps entre les arrivées, on obtient la probabilité de passer de l'état \(i\) à l'état \(i - 1\) et l'élément de matrice \(g_{i, i - 1}\) qui est égal à \(\mu\).
Aucune transition
Dans un intervalle de temps donné, trois choses peuvent se produire : une arrivée, un départ, ou rien du tout. S'il ne se produit rien, la chaîne de Markov demeure à l'état \(i\). La somme des probabilités doit être 1 donc
et l'élément de matrice est \(g_{ii} = -(\lambda + \mu)\).
Aperçu du générateur
On connaît maintenant tous les éléments du générateur :
Pour la première ligne, il suffit de reconnaître que s'il n'y a aucun client dans la queue, les deux seuls événements qui peuvent survenir sont une arrivée ou rien du tout.
Distribution stationnaire
Le générateur contient toute l'information sur les transitions dans la chaîne. À partir de n'importe quelle longueur de queue initiale, il est possible de déterminer la distribution de probabilité de la longueur de queue à n'importe quel instant. Il existe un résultat intéressant (et un peu étonnant) qui garantit que la chaîne va converger vers une distribution unique peu importe l'état initial. Pour l'instant, supposons qu'une telle distribution existe, et nous verrons un peu plus tard sous quelles conditions cela est vrai.
Si la chaîne est dans une distribution stationnaire \(\pi\) (\(\pi\) est un vecteur infini dont l'élément à la position \(i\) indique la probabilité que la queue ait une longueur \(i\), \(i \geq 0\)), à n'importe quel instant ultérieur, elle est toujours dans la même distribution. Autrement dit, la probabilité de changer la distribution est nulle. En langage matriciel, on peut traduire ce fait par
En écrivant les premières équations de ce système, il est facile de déduire la distribution stationnaire :
donc
et en se rappelant de la définition de l'intensité du trafic, on a simplement
La seconde équation donne
On peut montrer par induction que
Nous sommes maintenant en mesure de déterminer sous quelle condition la distribution stationnaire existe. Pour que \(\pi\) soit une distribution de probabilité, il faut que la somme de tous ses éléments soit égale à 1 :
Or, cette série est une série géométrique et une telle série ne converge que si son argument, ici \(\rho\), est inférieur (en valeur absolue) à 1. Autrement dit, une distribution stationnaire n'existe que si l'intensité du traffic est inférieure à 1, ce qui confirme notre intuition du départ.
Pour la suite, on suppose que l'intensité du trafic est inférieure à 1, et donc que la distribution stationnaire existe. Pour la déterminer, on commence par obtenir \(\pi_0\), puis on obtient l'ensemble de la distribution grâce à la relation obtenue plus haut. D'abord
donc
Par substitution,
Longueur moyenne de la queue
Si la chaîne de Markov a atteint la distribution stationnaire, on peut facilement calculer la longueur moyenne de la file d'attente et le temps d'attente moyen pour chaque client. La longueur moyenne de la file d'attente est donnée par
La somme n'est autre que la dérivée par rapport à l'argument d'une série géométrique, donc
Par exemple, si l'intensité du trafic est de 0.5 et que la file d'attente a atteint la distribution stationnaire, la longueur moyenne de la file d'attente est d'un client. La figure ci-dessous montre la longueur de la queue en fonction de l'intensité du trafic.
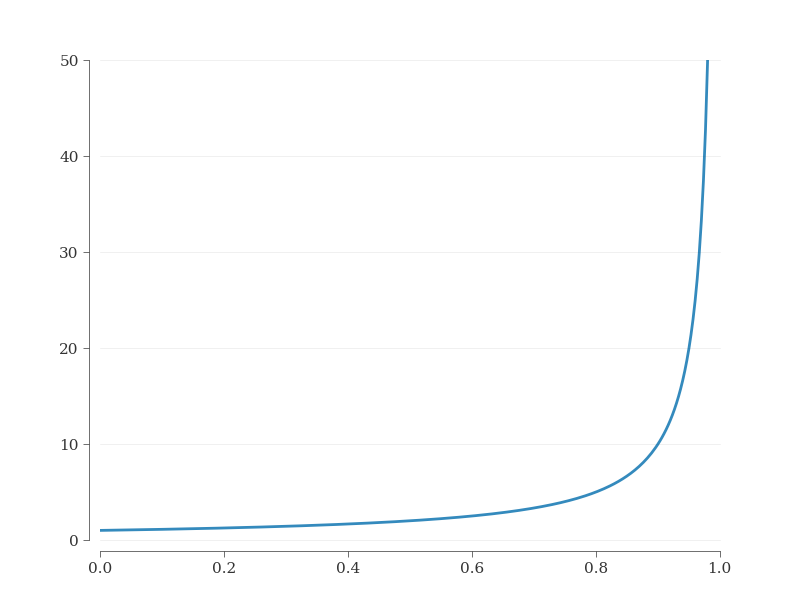
Quiconque conçoit un système dans lequel il y aura une queue a donc tout intérêt à s'assurer que l'intensité du trafic soit suffisamment loin de 1 pour ne pas que la file d'attente croisse indéfiniment.
Temps d'attente moyen
Lorsqu'un nouveau client arrive, chaque client déjà présent dans la file doit être servi avant que le nouveau client ne puisse l'être. En utilisant la linéarité de l'espérance, le fait que le temps de service soit une exponentielle et la distribution stationnaire, on trouve que le nouveau client devra attendre en moyenne
Conclusion
L'étude du comportement des files d'attentes est très complexe. Le modèle que nous avons exploré dans cet article est très simple, et même dans ce cas, il est difficile d'obtenir des informations utiles si le système n'a pas atteint sa distribution stationnaire. L'utilisation même de la distribution stationnaire n'est pas toujours appropriée en pratique (un gérant de magasin Apple doit prévoir que la longueur de la file d'attente à l'ouverture le jour du lancement du iPad 12 peut être très longue, et que la journée entière ne sera peut-être pas suffisante pour atteindre la distribution stationnaire).
Néanmoins, les résultats théoriques obtenus ici permettent une première approximation qui peut être utile. Cette approximation peut par la suite être raffinée en utilisant des simulations.