Le principe de conservation de la masse stipule que la masse totale d'un système fermé est un invariant, c'est-à-dire qu'elle est constante dans le temps. Si le système étudié est un fluide, ce principe mène à l'équation de conservation de la masse aussi connue sous le nom d'équation de continuité :
Dans ce contexte, la conservation de la masse signifie que pour n'importe quelle région de l'espace, la masse de fluide contenue à l'intérieur de cette région ne peut changer que si du fluide est passé à travers l'interface entre cette région et le reste de l'espace. Autrement dit, il faut que quelque chose (une masse de fluide) soit entré ou sorti.
Le but de ce billet est de présenter les détails de la dérivation de cette équation.
Définition des quantités physiques
Il existe deux approches pour décrire un fluide. Dans la première, eulérienne, le fluide se déplace par rapport à un système de référence fixe. Les quantité physiques qui caractérisent le fluide sont des champs scalaires (comme pour la température) ou vectoriels (pour la vitesse) qui dépendent du temps et de la position dans l'espace \(\mathbf{r}\). La seconde approche, lagrangienne, consiste à suivre le mouvement d'un élément de fluide. Cet élément est caractérisé par une position \(\mathbf{\xi}\) qui dépend du temps. Dans ce billet, l'approche eulérienne est utilisée.
La densité de masse du fluide varie dans le temps et dans l'espace : \(\rho = \rho(t, \mathbf{r})\). Le champ de vitesse \(\mathbf{u}(t, \mathbf{r})\) décrit la vitesse de l'élément de fluide qui se trouve à la position \(\mathbf{r}\) au temps \(t\).
L'espace est divisé en deux par une surface fermée \(S\) qui englobe une région de volume \(V\). À chaque élément de surface correspond un vecteur \(d\mathbf{a}\) dont la longueur est l'aire de l'élément de surface, et la direction est perpendiculaire au plan tangent à la surface et vers l'extérieur. La figure ci-contre illustre ces différentes quantités.
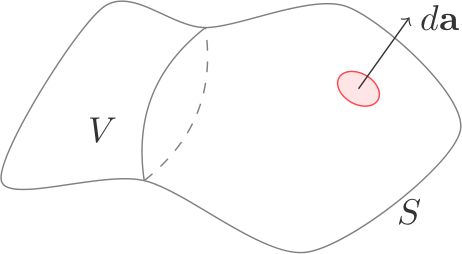
Un élément de surface \(d\mathbf{a}\) d'une surface fermée \(S\) qui définit un volume \(V\).
Si \(\mathbf{\hat{n}}\) est un vecteur unitaire perpendiculaire à la surface et pointant vers l'extérieur, alors \(d\mathbf{a} = \mathbf{\hat{n}} da\) où \(da\) est l'aire de l'élément de surface. Cette représentation sera utile pour la suite.
Changement de masse dans le volume
La masse totale dans le volume \(V\) est une quantité qui peut varier dans le temps : \(M = M(t)\). Cette masse est obtenue en intégrant la densité sur la totalité du volume :
Pour déterminer le taux de variation (instantané) de la masse en fonction du temps, il suffit de dériver cette équation par rapport au temps :
En supposant que toutes les fonctions et les surfaces sont lisses et que l'intégrale converge (ce qui est toujours le cas, sauf peut-être dans les trous noirs), il est possible d'inverser l'ordre de la dérivée et de l'intégrale du côté droit de l'égalité. La masse de fluide contenue dans le volume \(V\) varie donc selon
La dérivée temporelle a été remplacée par une dérivée partielle parce que la densité, par opposition à la masse totale de fluide dans le volume \(V\), dépend non seulement du temps, mais aussi de la position.
Masse de fluide qui traverse la surface
La masse qui traverse la surface par unité de temps, appelée le flux de masse, dépend à la fois de la densité et de la vitesse du fluide. Il faut étudier l'effet de chacune de ces deux quantités sur le flux.
Si le fluide se déplace très rapidement, une plus grande quantité de matière devrait traverser la surface que s'il se déplace lentement. Cependant, il est possible que le fluide se déplace parallèlement à la surface, auquel cas la magnitude de la vitesse n'a aucune incidence sur le flux de matière qui traverse la surface. L'angle entre le vecteur vitesse et la surface joue donc un rôle important : seule la composante de cette vitesse qui est perpendiculaire à l'élément de surface contribue au flux. Par conséquent, la composante de la vitesse à considérer est \(\mathbf{u} \cdot \mathbf{\hat{n}}\).
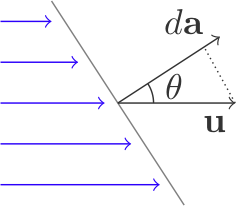
Au premier ordre, la vitesse du fluide est constante partout sur un élément de surface infinitésimal \(\mathbf{\hat{n}}da\). De plus, à une distance suffisamment petite de l'élément, la vitesse est approximativement constante. Dans un temps très court \(\Delta t\), seul le fluide situé dans un cylindre de section \(da\) et de longueur \(\Delta t \mathbf{u} \cdot \mathbf{\hat{n}}\) traverse l'élément de surface. Puisque \(da\) et \(\Delta t\) sont infinitésimaux, la densité de masse est constante dans ce cylindre et la masse qui y est contenue est donc \(\rho \Delta t \mathbf{u} \cdot \mathbf{\hat{n}} da\). Cette masse traverse la surface en un temps \(\Delta t\), d'où un flux de masse de \(\rho \mathbf{u} \cdot \mathbf{\hat{n}} da\) qui peut s'écrire de façon légèrement plus compacte comme \(\rho \mathbf{u} \cdot d\mathbf{a}\).

Le flux total à travers la surface s'obtient simplement en intégrant le flux à travers chaque élément de surface :
Il est important de noter que l'orientation de l'élément de surface \(d\mathbf{a}\) vers l'extérieur fait en sorte que le flux ci-dessus est interprété comme sortant de la surface s'il est positif et entrant dans la surface s'il est négatif.
Équation de continuité
Par conservation de la masse, toute matière qui traverse la surface doit contribuer à faire augmenter ou diminuer la masse contenue dans le volume \(V\). Il faut donc que le changement de masse dans le temps soit strictement égal au flux de masse à travers la surface. Avec la convention de signe adoptée plus haut, un flux sortant est positif et correspond à une diminution de la masse à l'intérieur de la surface et donc à une dérivée négative. Par conséquent, on obtient la relation suivante :
Le côté droit de l'égalité peut se récrire comme une intégrale de volume en utilisant le théorème de Gauss (ou de la divergence).
Puisque cette égalité doit être valide pour n'importe quel volume \(V\), il faut que les intégrands soient identiquement égaux, i.e. :
Conclusion
L'équation de continuité s'obtient relativement simplement à partir de considérations physiques simples. Même si la dérivation présentée ici a été faite dans le contexte de l'hydrodynamique, il est intéressant de noter que le raisonnement est aussi valable dans un grand nombre d'autres contextes. Par exemple, si la densité de masse est remplacé par une densité de charge, alors le produit \(\rho\mathbf{u}\) devient une densité de courant et l'équation est l'équation de conservation de la charge en électrodynamique.