Loïc Séguin-C.

On peut représenter les objets tridimensionnels par des triangles collés les uns aux autres de telle sorte qu'ils épousent les formes de l'objet. On appelle une telle construction une triangulation. Une fois qu'on a obtenu une triangulation, on peut la raffiner en divisant les triangles en triangles plus petits. Cet article présentera des méthodes de raffinement qui, lorsqu'on représente graphiquement les triangles qu'elles produisent, génèrent des dessins dont la beauté surprend.

Raffiner une triangulation

De l'animation par ordinateur au design d'aéronefs en passant par l'imagerie médicale, les applications de l'imagerie tridimensionnelle sont multiples. Les logiciels utilisés dans ces applications nécessitent une représentation d'objets tridimensionnels dans un langage compréhensible pour un ordinateur. On se heurte alors au problème de trouver un compromis entre une représentation fidèle de l'objet initial et une utilisation raisonnable des ressources matérielles de l'ordinateur : processeur, mémoire vive, espace de stockage sur disque dur, etc. Une méthode fréquemment utilisée consiste à trianguler la surface de l'objet, c'est-à-dire à recouvrir le mieux possible la surface de l'objet par des triangles, puis à raffiner cette triangulation initiale pour obtenir une meilleure représentation

des courbes de cette surface. On arrête de raffiner lorsque les calculs impliqués deviennent trop exigeant pour l'ordinateur. L'image ci-contre montre un exemple d'un objet tridimensionnel, une tête, et de trois triangulations de celle-ci. Les deux triangulations de droite sont des raffinements de celle de gauche. Les raffinements comptent beaucoup plus de triangles et semblent épouser les contours du visage beaucoup mieux.

Raffinement par division de triangles

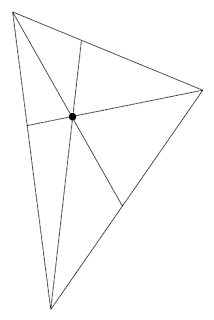
Une idée qu'on peut exploiter pour raffiner une triangulation consiste à diviser chacun des triangles existants en plusieurs triangles. En choisissant un point à l'intérieur d'un triangle et en faisant passer des droites par ce point et par chacun des sommets, le triangle initial est divisé en six triangles plus petits. En appliquant cet algorithme simple, qui est illustré ci-dessous, à une triangu lation, on obtient un raffinement. Chaque fois qu'on répète cette division, le nombre de triangle est multiplié par six. Donc après k itérations (i.e. : répétitions), le nombre de triangles initial est multiplié par 6^k.

Il existe une infinité de choix pour le point à l'intérieur du triangle. Chacun de ces choix engendrera des triangles différents. En général, les triangles longs et étroits sont moins utiles pour représenter des courbes. On leur préfère des triangles plus semblables à un triangle équilatéral. Il faut donc à trouver un point spécifique à l'intérieur du triangle qui servira à le diviser et qui engendrera le plus possible des triangles "presque" équilatéraux.

Une représentation abstraite de tous les triangles par un triangle

Un résultat élémentaire de géométrie euclidienne dit que tous les triangles qui ont les mêmes angles sont semblables ; c'est-à-dire que si deux triangles ont les mêmes trois angles, un de ces triangles est un agrandissement de l'autre. On appelle une homothétie l'agrandissement ou le rapetissement qui permet de passer d'un triangle à l'autre. Puisque l'objectif de nos raffinement est de trouver des triangles qui sont proches d'un triangle équilatéral, on n'a pas à se soucier de la taille de ces triangles, tout ce qui compte, ce sont les trois angles. En somme, à une homothétie près, tous les triangles sont spécifiés uniquement par leurs trois angles. La somme des angles d'un triangle est 180° et chaque angle est compris entre 0° et 180° exclusivement. Si on nomme les angles x, y et z, on aura donc :

0 < x < 180
0 < y < 180
0 < z < 180
x + y + z = 180

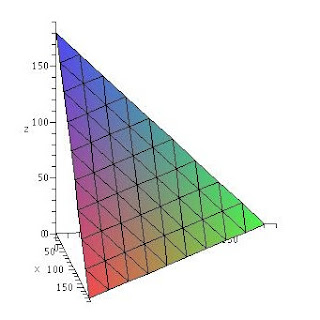
On peut interpréter les angles comme trois coordonnées dans l'espace cartésien en trois dimensions. Les points de l'espace cartésien qui correspondent aux quatre contraintes ci-haut forment une section de plan de forme triangulaire que nous appellerons T (voir figure ci-contre). Ce sous ensemble de l'espace cartésien est donc une représentation abstraite de tous les triangles imaginables. Le point central de T est le triangle équilatéral. Les points proches des côtés de T sont des triangles dont au moins un angle est très petit et qui sont donc très allongés.

Histogrammes de raffinement

On peut choisir un triangle et un point donné à l'intérieur des triangles pour faire un raffinement. On raffine notre triangle initial un grand nombre de fois pour obtenir plusieurs petits triangles. Chacun de ces petits triangles peut être représenté par un point noir dans T. Selon le nombre de triangles présents dans chaque région de T, il y aura plus ou moins de points noirs et on obtiendra une région plus ou moins sombre. L'image qu'on obtient est un histogramme de densité de points.

Ci-dessous se trouvent des histogrammes obtenus à partir de différents points à l'intérieur des triangles. On retrouve, dans l'ordre, la méthode de la bissectrice, la méthode du point de Gergonne et la méthode du point de Lemoine. (Ces images ont été obtenue grâce à la courtoisie de Steve Butler.)

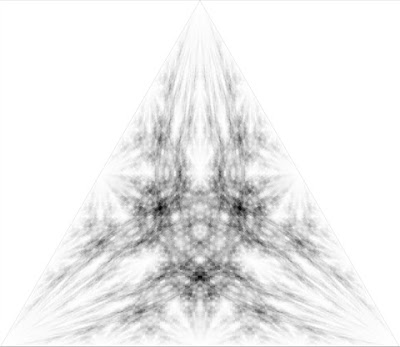
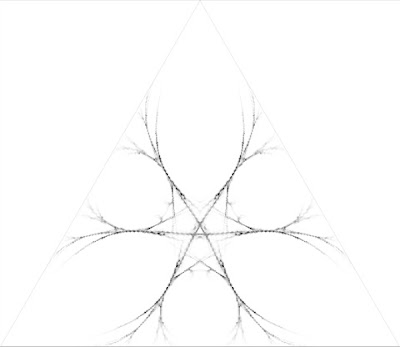
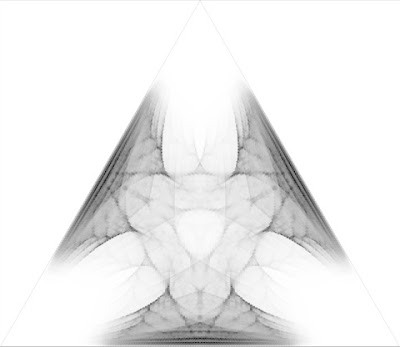
En plus d'avoir une certaine qualité esthétique, ces images donnent de l'information sur l'utilité des points intérieurs utilisés. On constate que pour la méthode de la bissectrice, le centre de T est assez sombre donc beaucoup de triangles presque équilatéraux sont produits ce qui est excellent.

Le point de Gergonne donne un histogramme qui ressemble à un neurone. Les points sont concentrés dans une toute petite région ce qui signifie que les triangles obtenus ont tous une forme bien particulière. Même si le point de Lemoine est le moins utile pour faire des raffinements en raison du grand nombre de triangles étroits qu'il produit (en effet, on constate que les côtés de T sont sombres), c'est celui qui génère, à mon avis, le plus bel histogramme.

La transformation de T

À la section précédente on s'est intéressé à l'effet d'un choix de point intérieur sur un triangle donné après un grand nombre d'itération. On peut aussi examiner l'effet de ce choix sur l'ensemble de T après une itération. L'algorithme prend des triangles de T et les envoie vers d'autres triangles de T : il modifie donc complètement l'ensemble des triangles. On peut visualiser ce qui se passe en divisant T en plusieurs régions (qu'on prend triangulaire parce qu'il est plus facile de diviser un triangle en triangles plutôt qu'en dodécagones) qu'on colore en noir et blanc. Puis, on applique l'algorithme à tous les triangles et on observe où les triangles fils obtenus se retrouvent dans T. En gardant les mêmes divisions et les mêmes colorations, on obtient une carte de la disposition des triangles fils. Ci-dessous, dans l'ordre, T divisé en régions, la méthode du point de Gergonne, la méthode du point de Lemoine et la méthode de la médiane. (Images courtoisie de Steve Butler.)

Conclusion

Les histogrammes obtenus par le raffinement de triangulations ressemblent à des dessins au fusain. On y retrouve une symétrie évidente, des dégradés surprenant et des formes étrangement organiques. Les diagrammes des transformations de T font penser à certaines gravures d'Escher.